domingo, 30 de noviembre de 2014
sábado, 29 de noviembre de 2014
SEMBLANZA
Soy Marco A. Chávez Villegas originario de Querétaro, curse 2 años la Licenciatura en Diseño Gráfico en la Universidad Autónoma de Querétaro, Actualmente soy estudiante de Ingeniería en Sistemas Computacionales en el I.T.Q, el cambio de carrera fue porque encontré lo que realmente quiero hacer en mi vida.
Soy Hector Becerra Mondragón egresé del Cobaq #2 Amealco, Querétaro. Lo que me motivo para estudiar Ingeniería en Sistemas fue mi tío, él estudio lo que ahora estoy estudiando, gracias a mi “no decisión de que estudiar” creo que fue una buena opción, me considero apasionado de la música, no solo es oirla, es traerla puest a través de tus ropas, peinados, frases, conductas, etc.
Luis giovanni Rocha Carrizales, originario de Tula Tamaulipas, estudie la preparatoria en San Luis de la Paz, GTO, actualmente estudio Ingeniería en Sistemas Computacionales en el Instituto Tecnológico de Querétaro.
El gusto por las computadoras y todo lo relacionado nace durante mi estancia en la preparatoria, aunque mi mayor pasión son los deportes, sobre todo el ¡futból! el cual practico a nivel de fuerzas básicas.
TABLA DE CONTENIDO
Portada
Semblanza
Tabla de Contenido
Temas:
Relaciones
Teoría de Grafos.
Reflexión
Conclusiones
APORTACIONES
INTRODUCCIÓN
El objetivo principal de este blog es brindar información de los temas "RELACIONES" y "TEORÍA DE GRAFOS" en materia de Matemáticas Discretas.
El contenido de este blog esta apoyado en distintas fuentes de información (internet, libros, videos, etc.)
viernes, 28 de noviembre de 2014
RELACIONES
5.1 CONCEPTOS BASICOS PAREJA ORDENADA
5.1.1 PRODUCTO CARTESIANO
5.1.2. RELACIÓN BINARIA
5.1.3 REPRESENTACION DE RELACIONES
5.2 PROPIEDADES DE RELACIONES
5.3 RELACIONES DE EQUIVALENCIA
5.4 FUNCIONES (INYECTIVA, SUPRAYECTIVA, BIYECTIVA)
5.5 APLICACIONES DE LAS RELACIONES Y LAS FUNCIONES EN LA COMPUTACIÓN
DEFINICIÓN
Las relaciones generalizan el concepto de funciones. La presencia del par ordenado (a, b) en una relación se interpreta como que existe una relación de a a b. El modelo de base de datos relacional que ayuda a los usuarios a tener acceso a la información de una base de datos (una colección de registros manejados por una computadora) se basa en el concepto de relación.
5.1 CONCEPTOS BASICOS PAREJA ORDENADA.
Esta relación se puede denotar de diversas formas:
1- Como pares ordenados (a, b).
2- Indicando que aRb.
3- Como una mezcla entra los dos anteriores R(a,b).
Al conjunto de todos los elementos relacionados mediante la relación R en un conjunto lo denotamos como R(M)
Está relación dependiendo del conjunto puede referirse a cualquier concepto referido con el conjunto.
Ejemplo: Sea el conjunto A={el conjunto de los números naturales}, una relación binaria del conjunto de A sobre sí mismo puede ser, R= ser múltiplo de.
De tal forma que, por ejemplo 4 está relacionado con 2 (es decir, 4 es un múltiplo de 2), por tanto escribimos 4R2 o (4,2). En el caso de no estar relacionados escribiremos a no está relacionado con b tachando la R. Un ejemplo de dos elementos que no están relacionados con esta relación son 3 y 5.
Observación: El conjunto R(AxB) de todos los elementos que están relacionados es un subconjunto del producto cartesiano AxB. (FUENTE)
Subir
5.1.1 PRODUCTO CARTESIANO
Es la relación entre los elementos de un conjunto con los otros elementos de otro conjunto. Como los polinomios.
Ejemplo:
A = {a, b}, B= {1, 2, 3}
A•B= {(a, 1); (a, 3);(b, 2); (b, 3)}
Subir
5.1.2. RELACIÓN BINARIA
Una relación binaria R se define generalmente como una terna ordenada donde X e Y son conjuntos arbitrarios, y G es un subconjunto del producto cartesiano X Y. Los conjuntos X e Y son llamados el dominio y codominio, respectivamente, de la relación, y G se llama su gráfica.
El estado de cuenta? R se lee "x está relacionado con R y", y se representa por xRy o R. La última anotación corresponde a la visualización de R como la función característica de "X" x "Y" para el conjunto de pares de G. El orden de los elementos en cada par de G es importante: si un? b, entonces aRb y el sujetador puede ser verdadera o falsa, independientemente uno de otro.
Una relación tal como se define por el triple se refiere a veces como una correspondencia en su lugar. En este caso la relación de X a Y es el subconjunto G XY, y "de X a Y" siempre debe ser especificado o implícito en el contexto cuando se hace referencia a la relación. En la práctica, la correspondencia y las relaciones tienden a ser utilizados indistintamente.
Subir
5.1.3 REPRESENTACION DE RELACIONES (Matrices, Conjuntos, Grafos, Diagrama de Flechas
Matrices
Un método para el estudio de las relaciones de manera algorítmica es utilizando matrices compuestas de ceros y unos. Definición:
Sean A y B conjuntos finitos de la forma:
Si R es una relación de A en B. La relación R puede ser representada por la matriz , donde La matriz se denomina matriz de R. En otras palabras la matriz, de ceros y unos, de R tiene un 1 en la posición cuando está relacionado con , y un 1 en está posición si no está relacionado con . Obsérvese en la definición anterior que los elementos de A y B han sido escritos en un orden particular pero arbitrario.
Por lo tanto, la matriz que representa una relación depende de los órdenes usados para A y B.
Cuando A = B usamos el mismo orden para A y B. Ejemplo:
Sean . Consideremos la siguiente relación de :
Entonces la matriz de R es Recíprocamente, dando los conjuntos A y B con m y n elementos respectivamente, una matriz de m x n formada de ceros y unos determina una relación de A en B, como se ilustra en el siguiente ejemplo. Ejemplo:
Determinemos las parejas ordenadas que están en la relación R representada por la matriz Puesto que R consiste de aquellas parejas ordenadas , con , se sigue que
Representación de relaciones usando conjuntos. Un conjunto es una colección de objetos considerada como un objeto en sí. Los objetos de la colección pueden ser cualquier cosa: personas, números, colores, letras, figuras, etc. Cada uno de los objetos en la colección es un elemento o miembro del conjunto.
Por ejemplo, el conjunto de los colores del arcoíris es: AI = {Rojo, Naranja, Amarillo, Verde, Azul, Añil, Violeta}
Un conjunto suele definirse mediante una propiedad que todos sus elementos comparten.
Por ejemplo, para los números naturales, si consideramos la propiedad de ser un número primo, el conjunto de los número primos es:
P = {2, 3, 5, 7, 11, 13, …}
Un conjunto queda definido únicamente por sus miembros y por nada más. En particular el orden en el que se representen estos es irrelevante. Además, cada elemento puede aparecer de manera idéntica una sola vez, esto es, no puede haber elementos totalmente idénticos repetidos.
Por ejemplo: S = {Lunes, Martes, Miércoles, Jueves, Viernes} = {Martes, Viernes, Jueves, Lunes, Miércoles} AI = {Rojo, Naranja, Amarillo, Verde, Azul, Añil, Violeta} = {Rojo, Naranja, Amarillo, Verde, Azul, Añil, Violeta, Naranja} Los conjuntos pueden ser finitos o infinitos.
El conjunto de los número naturales es infinito, pero el conjunto de los planetas en el sistema solar es finito (tiene ocho elementos). Además, con los conjuntos pueden combinarse mediante operaciones, de manera similar a las operaciones con números. Los conjuntos son un concepto básico, en el sentido de que no es posible definirlos en términos de nociones más elementales, por lo que su estudio puede realizarse de manera informal, apelando a la intuición y a la lógica.
Por otro lado, son el concepto fundamental de la matemática: mediante ellos puede formularse el resto de objetos matemáticos, como los números y las funciones, entre otros. Su estudio detallado requiere pues la introducción de axiomas y conduce a la teoría de conjunto Representación de relaciones usando grafos.
Un grafo es el principal objeto de estudio de la teoría de grafos. Informalmente, un grafo es un conjunto de objetos llamados vértices o nodos unidos por enlaces llamados aristas o arcos, que permiten representar relaciones binaria entre elementos de un conjunto. Típicamente, un grafo se representa gráficamente como un conjunto de puntos (vértices o nodos) unidos por líneas (aristas). Un grafo G es un par ordenado G = (V,E), donde:
• V es un conjunto de vértices o nodos, y • E es un conjunto de aristas o arcos, que relacionan estos nodos.
Normalmente V suele ser finito. Muchos resultados importantes sobre grafos no son aplicables para grafos infinitos. Se llama orden del grafo G a su número de vértices, | V | . El grado de un vértice o nodo V es igual al número de arcos E que se encuentran en él. Un bucle es una arista que relaciona al mismo nodo; es decir, una arista donde el nodo inicial y el nodo final coinciden. EJEMPLO:
• V:={1,2,3,4,5,6} • E:={{1,2},{1,5},{2,3},{2,5},{3,4},{4,5},{4,6}}
El hecho que el vértice 1 sea adyacente con el vértice 2 puede ser denotado como 1 ~ 2. • En la teorías de las categorías una categoría puede ser considerada como un multigrafo dirigido, con los objetos como vértices y los morfismos como aristas dirigidas. • En ciencias de la computación los grafos dirigidos son usados para representar máquinas de estado finito y algunas otras estructuras discretas.
Una relación binaria R en un conjunto X es un grafo dirigido simple. Dos vértices a, b en X están conectados por una arista dirigida ab si aRb.
Representación de relaciones usando diagramas de flechas.
Una forma de representar el producto cartesiano es el diagrama de flechas. Escriba los elementos de a y los elementos de b en dos discos disyuntos, y luego dibuje una flecha de ” a e a “ en ” b e b” cada vez que a este relacionado con b.
Subir
5.2 PROPIEDADES DE RELACIONES
Definición:
Una relación
Sea A = {1, 2, 3, 4} y sean
R1 = {(1, 1), (1, 2), (2, 1), (2, 2), (3, 4), (4, 1), (4, 4)}
R2 = {(1, 1), (1, 2), (2, 1)}
R3 = {(1, 1), (1, 2), (1, 4), (2, 1), (2, 2), (3, 3), (4, 1), (4, 4)}
R4 = {(2, 1), (3, 1), (3, 2), (4, 1), (4, 2), (4, 3)}
R5 = {(1, 1), (1, 2), (1, 3), (1, 4), (2, 2), (2, 3), (2, 4), (3, 3), (3, 4), (4, 4)}
R6 = {(3, 4)}
Ejemplo:
¿Cuáles relaciones son reflexivas? R3 y R5
Definición:
Una relación R sobre un conjunto A es llamada no reflexiva (o irreflexiva) si el par ordenado (a, a)
Ejemplo:
¿Cúales de las relaciones descritas no son reflexivas? R4 y R6
Mientras que R1 y R2 no relaciones que no son ni reflexiva ni no reflexivas.
Por medio de tablas podemos mostrar este tipo de relaciones.
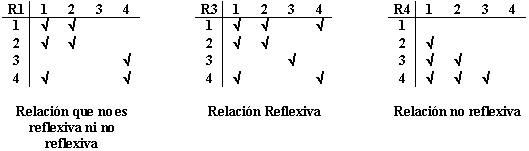
Una relación
Una relación
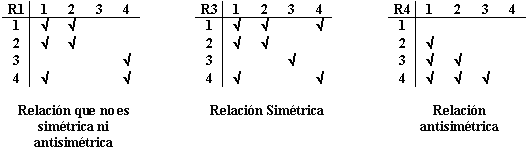
Definición:
Una relación
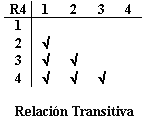
(3, 2) y (2, 1)
(4, 2) y (2, 1)
(4, 3) y (3, 1)
(4, 3) y (3, 2)
Un grafo dirigido de una relación transitiva tiene la propiedad que si existen aristas dirigidas de x a y y de y a z, también existe una arista dirigida de x a z. Como lo muestra el siguiente grafo
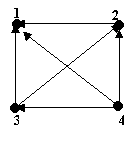
Sea
Ejemplo:
Sean A = {a, b, c, d} y
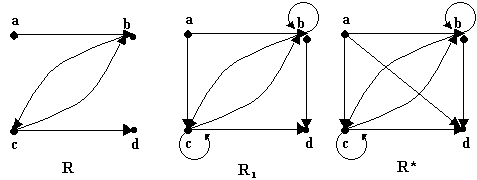
Subir
5.3 RELACIONES DE EQUIVALENCIA (CERRADURAS, CLASES DE EQUIVALENCIA, PARTICIONES)
CERRADURA REFLEXVA
Sea R una relacion en AxA la cerradura reflexiva de R es R ⊆ AxA tal que R es la relación mas pequeña que contiene R y es reflexiva.CERRADURA SIMÉTRICA
Sea R una relacion en AxA la cerradura simétrica de R es R ⊆ AxA tal que R es la relación mas pequeña que contiene a R y es simétrica.CERRADURA TRANSITIVA
Sea R una relacion en AxA la cerradura transitiva de R es R ⊆ AxA tal que R es la relación mas pequeña que contiene a R y es simétrica.VIDEO DE APOYO
PARTICIONES
Sea X un conjunto. P es una partición de X si y sólo si: Ø ∉ P UP = A Los conjuntos de P son disyuntos 2 a 2, es decir, si S1,S2 ∈ P y S1≠S2 entonces S1 ∩ S2 = Ø Observe que si P es una partición de X, entonces todo elemento de X está en uno y sólo un elemento S ∈ P uno y sólo un elemento de modo que parte a en conjuntos disyuntos. Por ejemplo, el conjunto de barriles propuesto al comienzo de la sección es una partición del conjunto de mangos. Otro ejemplo de una partición es de la división política de un país: El país (visto como un conjunto de personas) se parte en estados o departamentos no vacíos disyuntos entre sí. Ejemplo Sea ={1, 2, 3, 4, 5, 6, 7, 8, 9} Entonces = {{1, 9}, {2, 8}, {3, 4, 5, 6, 7}} Es una partición de X en tres conjuntos: elementos externos (1,9), elementos semi-externos (2, 8) y elementos internos (3, 4, 5, 6, 7). Note que Q = {{1, 2, 9}, {2, 8}, {3, 4, 5, 6, 7}} no es partición de X (¿por qué?). Como lo habíamos insinuado, resulta que toda relación de equivalencia determina de manera natural una partición.Subir
5.4 FUNCIONES (INYECTIVA, SUPRAYECTIVA, BIYECTIVA)
Función Inyectiva:
A una función en la que a cualquiera par de elementos diferentes del dominio les corresponde imágenes diferentes se le llama función inyectiva (significa uno a uno)Función Suprayectiva:
Si todo elemento del codominio de una función f es imagen de al menos un elemento de su dominio, entonces f es una función suprayectivaVIDEO DE APOYO
Subir
5.5 APLICACIONES DE LAS RELACIONES Y LAS FUNCIONES EN LA COMPUTACIÓN
Uno de los conceptos más importantes en Matemáticas es el de función, ya que se puedeaplicar en numerosas situaciones de la vida cotidiana, y determinar las relaciones que existen entre magnitudes tanto en Matemáticas, Físicas, Economía, etc., y poder calcular el valor de una de ellas en función de otras de las que depende. Ya desde hace años, se observaron fenómenos que estaban relacionados con otros, así el volumen de un gas a temperatura constante, está relacionado con la presión, la fuerza de atracción entre dos cuerpos se vio que estaba relacionada con la masa de esos cuerpos y la distancia que les separa, y el capital final de una inversión está determinado por el capital invertido y el tiempo que dure esa inversión, etc. APLICACIONES DE LAS FUNCIONES A DISTINTAS ÁREAS: En cualquier área de las ciencias, existen leyes en las que se relacionan distintas magnitudes, temperatura-presión, masa-velocidad, intensidad del sonido-distancia, etc. Es decir, a partir de los valores de algunas magnitudes se obtienen los valores de otras de forma directa a través de fórmulas ya demostradas. Un punto de origen del concepto de función nace precisamente de las relaciones que mantienen diferentes magnitudes, así pues la función se puede representar algebraicamente o de forma gráfica en la que se relacionan varias magnitudes entre sí. Mediante la representación gráfica de estas relaciones entre diferentes magnitudes, se pudo dar de forma visual esa relación e interpretarla de forma rápida y sencilla. Una forma de representación es la que se hace mediante ejes cartesianos, en la que se la función se representa de forma general por la relación numérica de magnitudes en una gráfica. Así pues, la función la podremos representar tanto gráficamente como mediante una expresión algebraica o fórmula. Euler fue el primero en emplear la expresión f(x) para representar una función f asociada a un valor x. Es decir, con esta representación que es empleada hoy, se comienza la utilización del concepto de función tal y como hoy se entiende.
Subir










